First of all, I’m not a mathematician, but an engineer who loves challenges. :).
I’m going to explain how I came to this topic by solving some interesting problems.
I’m starting this series with a challenge that has a nice graphical interpretation in 3-dimensional space.
Challenge 1
$a\sqrt{2} + b\sqrt{3} = 7.5959858026829237684897…$
Find coefficients a, b in $\Z$
Constraint: Coefficients should be small (say, from -256 to 256).
This can be quickly solved by Brute-force, but our topic is Lattice this time. And I want to explain how I think about it from Lattice perspective. And we can also easily extend the challenge to 20 coefficients, which makes the brute-force method effectively unusable.
An important note is that the square root of a prime is an irrational number (it cannot be expressed as a fraction of two integers). So each coefficient is multiplied by irrational number and result is also irrational.
If we want to solve similar challenge, but with rational numbers, for example:
$a\frac{2}{3} + b\frac{3}{4} = 8$.
we quickly find that there is infinite number of solution in $\Z$ ring. For any b we have corresponding a. And it holds for any rational numbers (fractions).
$\frac{8a + 9b}{12} = 8$.
$a = \frac{96 - 9b}{8}$
The same thing will happen if we round irrational numbers to a certain number of decimal digits; the coefficients will just be quite large, depending on the precision of the rounding.
So back to our irrational numbers which assure unique solution. We are trying to find coefficients a, b such as left side of given equation is as much as possible close to irrational number on right side.
And exactly this bolded expression brings Lattice topic to the scene:
Lattice introduction
There is a lot of articles and videos about Lattices, basis vectors and finding shortest (SVP) or closest(CVP) vector.
Awesome introduction video is for example here.
I do not want to write general introduction to Lattices in this post, but rather focus on explanation by example. I just point to few important things, how I understand them and how they are related to my challenge.
- I will talk exclusively about Lattices over Integers ($\Z$), Such Lattice is exactly what its names suggest - group of points in space with integer coordinates
- Important parameter of each Lattice is its dimension. Thus 2 or 3 dimensional Lattice is easy to imagine as some periodical structure in 2 or 3 dimensions. When I started with this topic, I tried to extend this image to higher dimensions, but it is hard. This is reason why my first challenge is with 2 coefficients and it really works also in higher dimensions.
- Lattice structure is always determined by basis vectors. In two dimensional space by two linear vectors, in three dimensional by three linear vectors and so on.
- Non intuitive fact is, that all Lattices points can be always constructed from any basis vectors by infinite numbers of operations between basis vectors.
Lifting from irrational numbers to Integers.
As I want to work with Lattices over Integers ($\Z$), I need to “lift” irrational numbers $\sqrt{2}$ and $\sqrt{3}$ to Integers. So I need to multiply them by some lifting coefficient (say M), then round and make it integer. Precision of rounding by lifting depends on two factors:
- How big could be coefficients, which are we trying to find. I have constrain them up to 256 in my challenge. Larger coefficients require higher rounding precision, which in turn means a larger M.
- How many coefficients (and irrational numbers) are in challenge. We have just 2. But more coefficients require bigger precision of rounding and again bigger M.
It is simple - as bigger coefficients are allowed and the more we have them, the density of possible solutions around the real solution increases, and we need to distinguish between close possible solutions and the real solution.
For the current toy challenge lifting and rounding by $M = 10^3$ will be enough. But based on my experience, when number of coefficients in challenge is about 20, we will need $M = 10^{45}$ to find correct solution (even when we are still trying to find small coefficients). In following calculations I will use $M = 10^{12}$ to clearly distinguish the real solution from other candidates.
Now we are prepared to proceed to cardinal task of the challenge.
Lattice construction for challenge
The most difficult task of any challenge, solvable by Lattice, is to Spot the Lattice
I drew how the basis vectors v1 (blue), v2 (green), and v3 (yellow) of my challenge could look in 3-dimensional space.
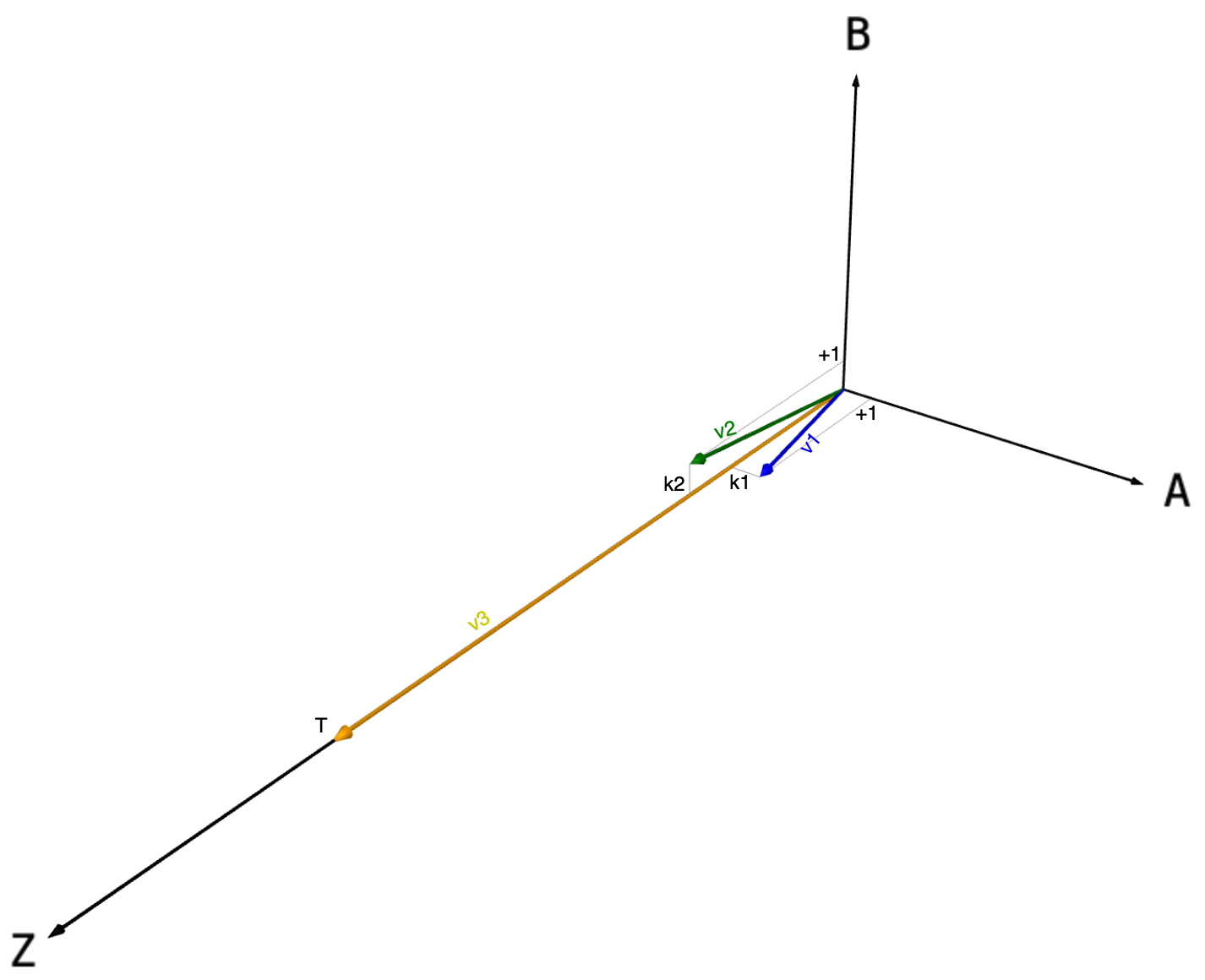 .
.
Where:
$M = 10^{12}$
k1 = $M\sqrt{2}$ rounded to integer
k2 = $M\sqrt{3}$ rounded to integer
I came to this by following thought process:
If all vectors lived only on the Z axis (purely one-dimensional), the question of finding a solution would be:
how many times should I multiply the lengths of v1 and v2 to get exactly the length of v3?
$a\vert\overrightarrow{v1}\vert + b\vert\overrightarrow{v2}\vert = \vert\overrightarrow{v3}\vert$
$a, b, \in \Z$, so they can be also negative of course
And now the key part.
I want to bring this idea to the lattice world by adding two more dimensions, A and B.
I do this by “shifting” vectors $\overrightarrow{v1}$ and $\overrightarrow{v2}$ to the side (each to its own axis).
Why?
- I want to create a basis for Lattice structure from 3 vectors, which is impossible with vectors in one dimension.
- The axes A and B will “track” the coefficients a and b (so I will know how many times to multiply the vectors by a and b).
- I can reformulate question to the more Lattice fashion’s question: “Find the vector closest to v3:
“Shift” of vectors $\overrightarrow{v1}$ and $\overrightarrow{v2}$ to side should be small against their length and value 1 is a good choice.
So finally our Lattice will be infinite structure of points in 3 dimensional space, where each point is some combination of basis vectors v1, v2, v3, where values of a and b will be tracked on Axis A and B
LLL - finding the solution.
The Second most important task after spotting and constructing “right” Lattice is to solve some of Lattice’s typical question. In our case:
“Find the vector’s combination closest to v3, with non-zero v1, v2:.
And exactly this kind of problem solves LLL (Lenstra-Lenstra-Lovasz) algorithm.
Actually, it tries to find the smallest non-zero vector in the given lattice structure, but this is a very similar problem. I just need to use a small trick with the negative sign of v3.
Let’s look to LLL as BlackBox for now and keep focus to challenge solution. We just need to know that LLL takes Lattice structure (defined by any basis’s vectors) structured in a matrix and try to find the smallest non-zero vector using mathematical operations over given vectors.
I will use SageMath tool to write Lattice matrix and solve it by LLL.
Calculation
Now comes the easiest part of the challenge: defining the vectors and matrix, and solving it using LLL in SageMath.
# unknown coefficients, which we will try to find, say:
a = -13
b = 15
sqrt2 = sqrt(2)
sqrt3 = sqrt(3)
target = a*sqrt2 + b*sqrt3 # this is known right side of our challenge
# lifting coefficient, I choose this one, but smaller will also work in this case
M = 10**12
# constructing vectors (note negative sign with vector v3)
v1 = vector([int(round(M * sqrt2)), 1, 0])
v2 = vector([int(round(M * sqrt3)), 0, 1])
v3 = vector([-int(round(M * target)), 0, 0])
# constructing final Lattice
B = Matrix([v1, v2, v3])
# applying LLL algorithm
B_lll = B.LLL()
print(B_lll)
And output is:
[ 3 -13 15]
[ 333326 -141751 -189521]
[ 468120 649131 468948]
In the first row, we can see a “nice small vector”, which points to the lattice point closest to [0, 0, 0]. The other points are much farther away, so we can be quite sure that this is our solution.
So answer to challenge is:
a = -13
b = 15
And final check:
sage: (-13*sqrt(2) + 15*sqrt(3)).n(80)
7.5959858026829237684897
What is exactly right side of challenge.
Conclusion
And that’s all.
This example shows how a simple problem in irrational combinations maps naturally into a lattice closest vector problem — and how tools like LLL can solve it efficiently.
I did my best and hope this will help someone.
In the next challenge, I’ll try to explain how to solve modular congruence using lattices.