In this post I’m going to tell you about another example of Lattice usage. It is inspired by famous breaking of Merkle–Hellman knapsack cryptosystem. And as in my previous article I’ll try to focus to explaining how to spot and construct Lattice in the real challenge.
I recommend to read my previous post, which provides good background to next reading.
History
Merkle–Hellman knapsack cryptosystem is based on general knapsack problem:
It was published in 1978, year after introduction of RSA. It was promising due to effective decryption and ease of implementation. But it was first broken in 1982 by Adi Shamir, co-author of RSA. And two years later by Lagarias and Odlyzko using newly developed LLL Lattice reduction.
How this cryptosystem works?
Each cryptosystem is based on some “hard problem”. Two of them dominate contemporary crypto world:
- Integer factorization
- Discrete Logarithm
Merkle–Hellman knapsack cryptosystem is based on another “hard problem” The Subset-Sum Problem :
There is a list of positive integers, say:
$M = [3, 4, 7, 11, 14, 21, 31, 45, 46]$
chosen
And you are given number, say:
$b = 70$
You should find subset of list $M$, where the sum of subset values gives $b$. It is considered to be a hard problem and it really is if number of values in list $M$ is big enough.
But as for all cryptosystems there should be some kind of magic key. And knowledge of this key allows quick solution of generally hard problem. Nobody without this secret shouldn’t solve the problem effectively.
Merkle and Hellman came with such key in form of superincreasing list of positive integers. This is simply sequence of positive integers, where each next is at least two times bigger then previous.
Mathematically precisely:
$M = (m_1, m_2, m_3, … m_n)$
is a superincreasing sequence of integers if:
$m_{i+1} >= \displaystyle\sum_{j=1}^{i} m_j$ for all members of $M$
Simply each next number should be bigger than sum of all previous numbers.
Example of such superincreasing sequence could be:
$M = [3, 7, 14, 30, 63, 150, 311]$
And in this case it is very easy to find subset for given number b by following algorithm.
M = [3, 7, 14, 30, 63, 150, 311] # random superincreasing list of positive integers
S = [] # subset of M, where sum of values gives b
b = 51 # given b, which is sum of unknown members of subset S
b_temp = b
for number in reversed(M): # for all numbers in M starting from end
if b_temp >= number: # if n is bigger or equal of tested value of M
S.append(number) # add new member of subset
b_temp = b_temp - number # set new b_temp
print(S)
and output is:
[30, 14, 7]
Distances between members assure easy solution. It is analogy to decimal numerical system - you can simple decompose number 11 011 110 to ones, tens, hundreds and so on.
So exactly such superincreasing list of positive integers (M) will be Alice’s private key, her secret magic to solve hard problem.
But how she can make this task difficult for somebody in the middle?
Modular congruencies looks like very promising choice. So Alice choose two secret big numbers A, B such as:
$ A, B > 2 m_n$
$gcd(A, B) = 1$
where $m_n$ is a last number of superincreasing sequence M.
And then compute
$n_i \equiv Am_i (mod B)$
for each value of M and create new sequence $N = (n_1, n_2, n_3… n_n)$
So wrapping Alice’s private list around modulo B makes new sequence N definitelly non-superincreasing.
Let’s take our example of short superincreasing sequence M = [3, 7, 14, 30, 63, 150, 311], choose two random primes A, B and then calculate new $N$
M = [3, 7, 14, 30, 63, 150, 311]
A = 773
B = 829
N = []
for value in M:
new_value = (A * value) % B
N.append(new_value)
print(f"N = {N}")
and output is:
N = [661, 437, 45, 807, 617, 719, 822]
Sequence N is public key.
And now Bob want to send some secret message to Alice. This message represent subset-sum of new public key, which Alice can publish to everyone. So secret message s could be for example:
$s = [1, 0, 1, 0, 1, 0, 1]$
Bob now encrypt this message using Alice’s public key to get encrypted message c:
c = 1*661 + 0*437 + 1*45 + 0*807 + 1*617 + 0*719 + 1*822
print(c)
or simply
c = vector(s) * vector(N)
print(c)
both gives:
2145
2145 is our subset-sum $c$.
And as we already know, it is generally hard to find which numbers from sequence $N$ gives us exactly this sum. So anyone can see value of $c$ along with public key N.
But Alice knows her secret $M$. And she also has its $A$ and $B$.
Alice can first solve subset-sum problem using following by formula:
$b = A^{-1}c (mod B)$
b = (inverse_mod(A, B) * c) % B
print(b)
output is
391
Here Alice computes b - sum of subset determined by Bob’s secret plaintext message s, BUT over her original superincreasing sequence $M$.
And as we show earlier, this is easy to compute:
M = [3, 7, 14, 30, 63, 150, 311] # private key - superincreasing sequence choosen by Alice
S = [] # recovered subset of M
s = [] # recovered message
b = 391 # we know this from: b = (inverse_mod(A, B) * c) % B
b_temp = b
for number in reversed(M):
if b_temp >= number:
S.append(number)
b_temp = b_temp - number
for value in M:
if value in S:
s.append(1)
else:
s.append(0)
print(f"s = {s}")
and output is exactly Bob’s secret message:
s = [1, 0, 1, 0, 1, 0, 1]
Why this decryption works?
$b \equiv A^{-1}c \equiv A^{-1}\displaystyle\sum_{i=1}^n s_i N_i \equiv A^{-1}\displaystyle\sum_{i=1}^n s_i A M_i. \equiv \displaystyle\sum_{i=1}^n s_i M_i (mod B)$
So through this congruence we can transpose secret message c to subset-sum b determined by plain message s over secret superincresing sequence M. And then easily recover message s by finding right values in original superincresing sequence.
Breaking Merkle–Hellman knapsack cryptosystem by Lattice.
Challenge 2
For given public key sequence:
$N = [661, 437, 45, 807, 617, 719, 822]$
and given encrypted message:
$c = 2145$
Find original cleartext message $s$ in form of list of 0 and 1
Recall solution from previous challenge in 3-dimensional space. We are going to move to 8 dimensional space now. Ready?
Imagine, that that on axis $Z$ there are all members of public key - List $N$. But we need to distinguish between vectors. So each vector is shifted to side in its own dimension and lies on axis $Z$ in all other dimensions.
So we have 7 vectors almost lying on axis $Z$, just slightly shifted to another dimension for tracking purposes.
And the last vector represent subset-sum (encrypted message) from our example. It lies directly on axis $Z$ without any shift.
Exactly like this Matrix:
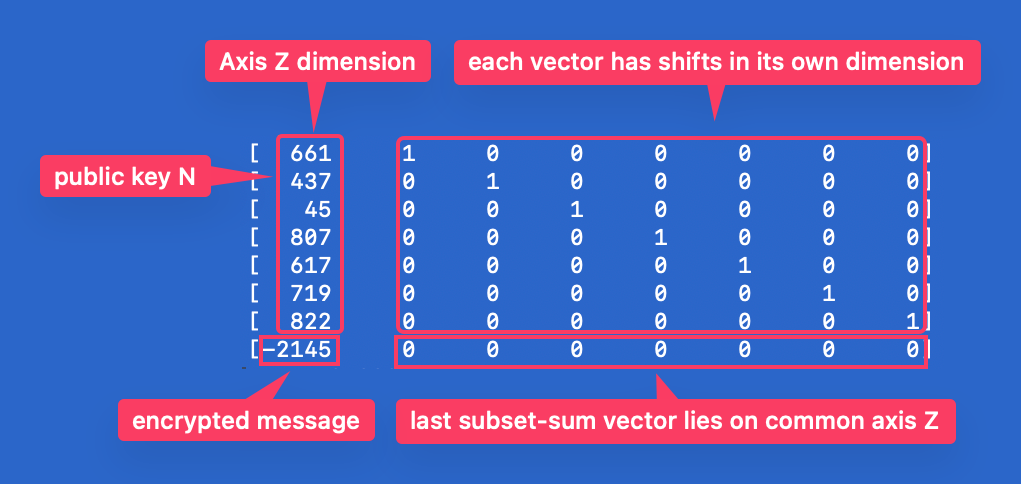
Why is the last subset-sum vector with negative sign?
Because we are going to use LLL method which tries to find the smallest non zero vector in given Lattice. So when we combine all “right” vectors (right values from list $N$) we should get exactly subset-sum. And if we subtract sum of right values and given subset-sum (encrypted message) we should get 0. So final vector after LLL transformation will have 0 in axis Z and smallest possible numbers (only 0 or 1) in all other dimensions.
Let’s try it in sage:
# construct Lattice, for given public key N and encrypted message c
N = [661, 437, 45, 807, 617, 719, 822]
c = 2145
l = len(N)
L = matrix(ZZ,(N)).T.augment(diagonal_matrix([1]*l)).stack(vector([-c,0,0,0,0,0,0,0]))
print(L)
output is exactly, what we wanted:
[ 661 1 0 0 0 0 0 0]
[ 437 0 1 0 0 0 0 0]
[ 45 0 0 1 0 0 0 0]
[ 807 0 0 0 1 0 0 0]
[ 617 0 0 0 0 1 0 0]
[ 719 0 0 0 0 0 1 0]
[ 822 0 0 0 0 0 0 1]
[-2145 0 0 0 0 0 0 0]
And now magic LLL algorithm:
L_lll = L.LLL()
print(L_lll)
with output:
[ 1 -1 0 1 0 1 0 0]
[ 0 1 0 1 0 1 0 1]
[ 0 1 0 -1 0 0 -2 1]
[ 1 1 0 1 -1 -1 1 0]
[-1 0 1 -1 -2 1 -1 -1]
[-2 0 1 2 1 -1 -1 0]
[-1 -2 0 -1 -2 1 1 2]
[ 1 -1 3 -1 0 0 1 1]
and in second row we see vector with 0 as we need and “nice small” vector with zeros and ones. 1 means that corresponding vector contribute to subset-sum, 0 means that this corresponding vector doesn’t contribute to to subset-sum.
Remaining values [1, 0, 1, 0, 1, 0, 1] are exactly Bob’s plaintext message s.
Conclusion
We went through another interesting type of challenge, where Lattices could be used. I tried to explain how to spot Lattice, how to construct and solve it.
Notes
- Some things were slightly simplified in order to better readability.
- Lattices has also its own limitation, LLL can solve matrixes up to small hundreds of dimensions