Learning with errors (LWE) is one of the cornerstone problems in modern lattice-based cryptography and algorithms based on LWE are most promising for post-quantum cryptography era.
I’m going to start this post with explanation of principles of LWE and then as usually in this series I’ll setup a challenge which I try to solve by Lattice and LLL algorithm. And again - I’ll focus on the practical process of creating a lattice. ;)
System of linear equations.
To be on the same page, I’d like to explain how to solve system of linear equations by matrix in Sagemath. Say that we have following system of just 4 equations with 4 unknowns:
$4a_1 + 5a_2 + 2a_3 + 7a_4 = 48$
$7a_1 + 6a_2 + 4a_3 + 3a_4 = 43$
$5a_1 + 2a_2 + 0a_3 + 3a_4 = 21$
$9a_1 + 6a_2 + 4a_3 + 2a_4 = 41$
In sage we can define left side of system as matrix $\bold{A}$:
A = matrix((
[4, 5, 2, 7],
[7, 6, 4, 3],
[5, 2, 0, 3],
[9, 6, 4, 2],
))
Right side we can define as vector $\overrightarrow{b}$:
b = vector([48,43,21,41])
Now we can find solution by sage operation:
A.solve_right(b)
And output is:
(1, 2, 3, 4)
Which is solution of given equations system. We can check first equation.
4*1 + 5*2 + 2*3 + 7*4
# 48
It is ok and I believe sage in this.
Switching to modulo.
Next step will be moving our linear system to modulo universe.
We need to define matrix over some integer ring. We can choose a simple integer modulo, or Gaussian field over prime. It doesn’t matter in this case, but let’s stay on safer side and choose modulo as a prime number and Gaussian Field for our next calculations. Choose modulo q = 23 and then matrix will be defined like this:
q = 23
A_gf = matrix(GF(q), (
[4, 5, 2, 7],
[7, 6, 4, 3],
[5, 2, 0, 3],
[9, 6, 4, 2],
))
Multiply it by expected solution:
A_gf * vector(GF(q), [1, 2, 3, 4])
# (2, 20, 21, 18)
And we get right side. And congruences (not equations anymore) will looks like:
$4a_1 + 5a_2 + 2a_3 + 7a_4 \equiv 2 \space\space mod(23)$
$7a_1 + 6a_2 + 4a_3 + 3a_4 \equiv 20 \space\space mod(23)$
$5a_1 + 2a_2 + 0a_3 + 3a_4 \equiv 21 \space\space mod(23)$
$9a_1 + 6a_2 + 4a_3 + 2a_4 \equiv 18 \space\space mod(23)$
We can check the first row:
(4*1 + 5*2 + 2*3 + 7*4) % 23
# 2
And it is ok.
Let’s check also 2. row for those who are more suspicious.
(7*1 + 6*2 + 4*3 +3*4) % 23
# 20
And it still holds.
We can employ sage’s solver to check complete congruence system:
b_gf = vector(GF(q), [2, 20, 21, 18])
A_gf.solve_right(b_gf)
And output is as expected:
(1, 2, 3, 4)
This was necessary introduction to solving linear equations and linear congruences by sage.
And we are ready to move to LWE now.
LWE introduction
Add 2 more congruences to our system to make it a bit overdetermined. I’ll explain why we need overdetermined system later.
$4a_1 + 5a_2 + 2a_3 + 7a_4 \equiv 2 \space\space mod(23)$
$7a_1 + 6a_2 + 4a_3 + 3a_4 \equiv 20 \space\space mod(23)$
$5a_1 + 2a_2 + 0a_3 + 3a_4 \equiv 21 \space\space mod(23)$
$9a_1 + 6a_2 + 4a_3 + 2a_4 \equiv 18 \space\space mod(23)$
$3a_1 + 5a_2 + 7a_3 + 9a_4 \equiv 1 \space\space mod(23)$
$0a_1 + 3a_2 + 6a_3 + 9a_4 \equiv 14 \space\space mod(23)$
A_gf = A_gf.stack(matrix(GF(q),([3, 5, 7, 9], [0, 3, 6, 9])))
A_gf * vector(GF(q), [1, 2, 3, 4])
# (2, 20, 21, 18, 1, 14)
b_gf = vector(GF(q), [2, 20, 21, 18, 1, 14])
A_gf.solve_right(b_gf)
# (1, 2, 3, 4)
System holds and everything is consistent.
But now try to inject small error to right side. Just change $2$ to $3$ in the first row.
And now try to solve by sage’s solver:
b_gf_err = vector(GF(q), [3, 20, 21, 18, 1, 14])
A_gf.solve_right(b_gf_err)
And we get error:
ValueError: matrix equation has no solutions
Expected. But the question is, if we are able to solve such intently broken overdetermined congruence system?
Indeed, it is a hard problem. Exactly what crypto systems need.
How hard depends on scale of errors and number of unknowns in congruence system.
Let’s formalize, what we just tested:
$\bold{A} \times \overrightarrow{s} + \overrightarrow{e} = \overrightarrow{b}$
Ok, and as in other crypto systems, we usually need public key, private key, plaintext message and encrypted message.
So what is what in LWE?
This is not exactly how LWE is used in cryptography, but it’s a useful mental model.
Public key is a matrix $\bold{A}$ - integer coefficients on left side of noisy congruence system.
Private secret key is vector of unknowns $\overrightarrow{s}$. $(a_1, a_2, a_3, a_4)$ in our case. We worked with 1, 2, 3, 4.
Plaintext secret message is vector of errors $\overrightarrow{e}$, which are injected to correct solution.
And right side, vector $\overrightarrow{b}$, we can consider as a cipher message.
With knowledge of private key (vector of unknowns of congruences system $\overrightarrow{s}$) it is straightforward to solve the system.
$\overrightarrow{e} = \overrightarrow{b} - \bold{A} \times \overrightarrow{s}$
We know everything what we need.
Without knowledge of private key, we have to try to solve noisy congruence system and try to identify injected errors.
I’ll try it in next section using Lattice method.
Creating Lattice on toy example
I’m going to construct Lattice for smallest possible example and explain it. Let’s start with just one unknown $x$ system.
$45x \equiv 51 \space\space mod(101)$
Now I inject error - modify the right side (+1) and I get a LWE congruence:
$45x \equiv 52 \space\space mod(101)$
There should be some $x$ and some $k$ for which the following statement is true:
$45 \times x - 52 - k\times 101$ is very close to 0
And really:
45*55 - 52 - 101*24
# gives -1
But there is one catch. If we calculate congruence:
$45x \equiv 51 \space\space mod(101)$ we get result $55$
But when we try:
$45x \equiv 52 \space\space mod(101)$
we get another result:
A = matrix(Integers(101),([45]))
b = vector(Integers(101),([51]))
A.solve_right(b)
# gives result 55
b = vector(Integers(101),([52]))
A.solve_right(b)
# gives result 64
In other words, there exists another $x$, which would give better result - shorter vector - then original $x$ tampered by a small error. This is exactly the reason why we need overdetermined system, to be able to find injected error.
And therefore another congruences are necessary to improve stability of system.
$45x \equiv 51 \space\space mod(101)$
$72x \equiv 21 \space\space mod(101)$
$12x \equiv 54 \space\space mod(101)$
Check it in sage:
45*55 %101 # gives 51
72*55 %101 # gives 21
12*55 %101 # gives 54
If we inject some small error to any congruence now, we should be able to reveal it, because the same $x$ and result close to 0 should hold across all 3 statements now:
$45 \times x - 51 - k\times 101$ is very close to 0
$72 \times x - 21 - k\times 101$ is very close to 0
$12 \times x - 54 - k\times 101$ is very close to 0
$k$ could be different in all 3 cases. $(k\times 101)$ is a “bridge” between modulo and $\Z$ worlds.
Finally we are getting to Lattice construction. Let’s say that we inject error just to first congruence. Say that error vector will be (1, 0, 0).
How will look like our 3 statements in Lattice then?
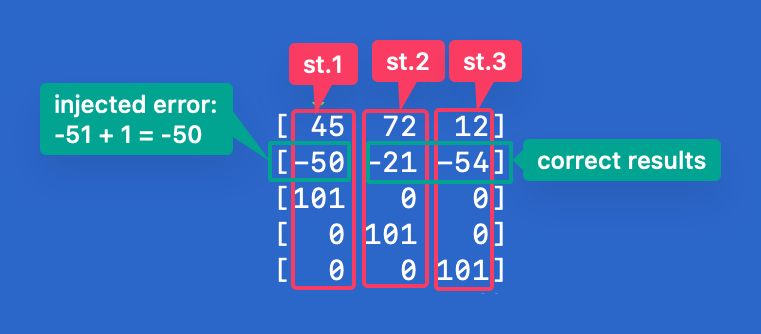
We can consider these 3 statements as 3 dimensions.
Each column represents one statement and LLL will try to find as smallest as possible non zero vector.
Important thing is it that it is still the same Lattice, but just with another basis, so $x$ should be still the same.
LLL is trying to find the best orthogonal basis and as a side effect if often finds also one very small small vector, which contains possible values in each dimension. And this vector is often wanted solution.
Let’s solve it in in sage:
A = matrix(([45, 72, 12], [-50, -21, -54], [101, 0, 0], [0, 101, 0], [0, 0, 101]))
A.LLL()
gives:
[ 0 0 0]
[ 0 0 0]
[ 1 0 0]
[ 0 -6 -1]
[ 0 5 -16]
And in 3nd row we can see our error vector.
Now we are ready to build a bit bigger system, so let try it in next challenge.
Challenge 3
Create noisy system with encoded message first
Let’s generate matrix with 64 columns and 96 rows with random coefficients over field $q = 2^{16} + 1$.
This matrix is a Public key.
Let’s generate Private key as vector of 64 random numbers.
Let’s choose plaintext message “HelloLattice” and encode it as 0 and 1 to error vector.
Calculate correct right side of system by multiplying matrix with secret vector.
Inject error vector to system - modified vector will be encrypted message.
$\overrightarrow{b} = \bold{A} \times \overrightarrow{s} + \overrightarrow{e}$
Challenge task:
Try to decrypt message without knowledge of private key.
First part is straightforward. Just follow challenge steps to create noisy system:
q = 2**16 + 1
m = 96 # rows
n = 64 # columns
# public key as matrix 96x64
A = Matrix(GF(q), m, n, lambda i, j: randint(0, q))
# private key as vector of 64 numbers:
s = vector(Matrix(GF(q), 1, n, lambda i, j: randint(0, q)))
# define plaintext message and encode it to error vector e:
message = "HelloLattice"
bits = [int(b) for c in message.encode("utf-8") for b in f"{c:08b}"]
e = vector(GF(q), bits)
# calculate correct right side of system:
b_correct = A * s
# and finally inject errors by adding correct right side and error vector:
b = b_correct + e
You can check all variables, but they are quite big, so I do not write outputs here.
With knowledge of private key the solution should be easy.
$\overrightarrow{e} = \overrightarrow{b} - \bold{A} \times \overrightarrow{s}$
Should give us cleartext message encoded in 0 and 1.
Let’s try it:
# calculate error vector - binary encoded message
e_exp = b - A * s
# and now try to decode
byte_values = []
for i in range(0, len(e_exp), 8):
byte = int("".join(str(b) for b in e_exp[i:i+8]), 2)
byte_values.append(byte)
print("Decoded message: ", bytes(byte_values).decode("utf-8", errors="ignore"))
And you should get correct plaintext message.
Now we continue with hardest way. We are going to recover message without knowledge of private key $\overrightarrow{s}$.
Solving challenge by Lattice
We know a system of linear equations (more precisely congruences), where right side is tampered by errors. We know that error could be 1 or 0, so very small divergence from correct results. Nothing else. This error vector is encoded plaintext message. So we want to find it. In this case error vector is 96 bits long. Even errors are small, it is still $2^{96}$ possibilities, which is completely infeasible by brute force method.
But keywords very small divergence from previous evaluation could lead us again to Lattice method.
In my case system of system of linear equations looks like this for better imagination.
$59521a_1 + 8581a_2 + 2477a_3 + … +11940a_{64} \equiv 25227 \space\space mod(65537)$
$47042a_1 + 23493a_2 + 2751a_3 + … + 60385a_{64} \equiv 23711 \space\space mod(65537)$
…
$21360a_1 + 18668a_2 + 62645a_3 + … + 57158a_{64} \equiv 21053 \space\space mod(65537)$
Number of rows is 96. As coefficients are random, they can vary each time of course. We know that:
$\bold{A} \times \overrightarrow{s} + \overrightarrow{e} = \overrightarrow{b}$
in my case:
$ \begin{pmatrix} 59521 & 8581 & … & 11940 \\ 47042 & 23493 & … & 60385 \\ … \\ 21360 & 18668 & … & 57158 \\ \end{pmatrix} \times \overrightarrow{s} + \overrightarrow{e} = (25227, 23711, …, 21053)$
LLL method can discover smallest non-zero vector in given Lattice, as in previous toy example. Note, that I’m building a Lattice from left to right:
$\bold A + \overrightarrow{b} + DiagonalMatrix$
And then transform matrix (rows <-> columns)
And other important note - I should switch matrix to $\Z$ ring.
Next steps are selfexplanating:
- finding row with small values
- testing solution by solving equations (note switching to modulo)
- decoding error vector to message
A_zz = matrix(ZZ, A)
b_zz = vector(ZZ, b)
A_aug = A_zz.augment(b_zz).augment(diagonal_matrix(ZZ, [q] * m)).T
A_lll = A_aug.LLL()
for row in A_lll:
if row != 0 and all(abs(x) <= 1 for x in row):
break
# solve the system
e_exp = vector(Integers(q), row)
try:
s_v = A.solve_right(b - e_exp)
print(f"*** System solvable: e = {e_exp}")
except:
print("No solution found with LATTICE method.")
s_v = None
byte_values = []
for i in range(0, len(e_exp), 8):
byte = int("".join(str(b) for b in e_exp[i:i+8]), 2)
byte_values.append(byte)
print("Decoded message: ", bytes(byte_values).decode("utf-8", errors="ignore"))
Conclusion
We looked at another beautiful usecase for Lattice LLL.
As it looks like some magic, but Lattices have also their limits.
Take challenge from this example and try to test bigger values in error vector, make system less overdetermined, or try to extend $\bold A$ matrix and you’ll find them quickly;).
Real LWE cryptosystems use carefully chosen parameters (large dimensions, Gaussian error) that make this lattice attack infeasible. But on toy systems, LLL works beautifully and demonstrates the principle.